Lecture-01 课程简介及算法分析
May 30, 2017
摘要: 1.介绍了算法性能分析的基本方法:渐进分析方法。 2.使用递归树的方法来求解递归问题的渐进复杂度。 3.介绍直接插入排序和归并排序两个例子。重点掌握归并排序算法的代码实现和时间复杂度分析。
1. 性能(performance)是算法分析最重要的内容¶
在算法导论这门课中,最最重点的就是要学会分析算法。而算法的性能(performance)或者叫运行效率,是算法分析的主要内容。对于一个软件来说,有很多方面都是需要程序员考虑的,比如正确性、可维护性、可扩展性、健壮性、安全性、用户交互性等等。对于一个软件是否成功,这些因素都是必须考虑的。但是为什么我们在这里要这么重点地去分析算法的效率呢?因为上面提到的很多方面其实都离不开运行效率,就笑课上老师打的一个比方:认为钱重要还是水和饭重要?当然是水和饭,钱是不能保证人的生存的,但是钱却可以换来水和饭。而算法分析中的“效率”就相当于“钱”,你可以用“效率”来换取其他东西,比如安全性,稳定性等等。它只是一个交换物,但我们,却离不开它。[1]
2. 衡量运行效率的因素¶
- 数据的输入情况。比如对于插入排序来说,一个已经排序好的序列更加容易排序。
- 数据的数量。比如短序列比长序列更好排序。
- 找到运行时间的上界。一般情况下,我们需要找到程序运行时间的上界来得到保证绝对不需要更长时间。
3. 几种分析运行时间的方法¶
- 最坏情况分析。 用T(n)来表示算法在输入规模为n时的最大运行时间。它的作用就是你可以用它来给别人做出承诺,即我的算法在最坏的情况下的运行时间也不会超过T(n)。
- 平均情况分析。 用T(n)来表示算法在输入规模为n时的期望运行时间。假设所有的输入符合均匀分布,计算所有输入所消耗的平均时间。
- 最优情况分析。 如果你想骗人,用一组极好的数据在一个效率极低的算法上跑,我们称之为算法的运行时间的最好情况,这是不够说服人的。
一般情况下都是进行最坏情况分析,而最优情况分析实际上没有任何意义。
4. 渐进分析¶
我们通常所说的运行时间,都会存在一个相对时间与绝对时间的区别。比如在一台巨型机和在一台微机上运行同一个程序,所用的时间显示是不同的。这是我们就需要引入一个更加宏观的概念:渐近分析
- 对于一个算法的运行时间,忽略那些依赖于机器的常量;
- 忽略所有的低阶项,只分析最高阶项;
- 关注于运行时间的增长,而不仅仅只是运行时间。不去考虑每个基本运算所消耗的时间。
4.1 渐进标注 $\Theta$ 标注¶
引入一个助记符号 $\Theta(n)$.
举一个例子:如果一个算法的运行时间为:$3n^3 + 2n^2 + 4n + 1$,那么忽略掉依赖机器的常量1,以及所有的低阶项 $2n^2$、$4n$,那么这个算法的时间复杂度就为$\Theta(n^3)$。
在这里,老师也进行了很形象的说明。如果算法A的渐近时间复杂度是$\Theta(n^3)$,算法B的是$\Theta(n^2)$,那么一定存在一个足够大的n,使得当数据规模大于n时,算法B的运行时间要小于A,不管算法A一开始的优势有多么大,不管算法B的渐近复杂度的系数和常数有多么大,都没有用。用这样一个助记符就可以将时间复杂度的分析独立于机器,独立于具体的常数,对我们分析算法将会十分有利。
5. 两个例子:插入排序、归并排序¶
5.1 插入排序¶
# 插入排序
def insert_sort(A, n):
"""A 为一个序列,n 为序列的长度。这里所有的下标都是从 0 开始,而课堂上从 1 开始。"""
for j in xrange(1,n): # 按照顺序从第二个元素开始逐个插入
key = A[j]
i = j - 1
while (i >= 0) & (A[i] > key):
A[i+1] = A[i]
i = i - 1
A[i+1] = key
return A
# Eg:
A = [8, 2, 4, 9, 3, 6, 7]
n = len(A)
print 'Before sorted: ', A
A = insert_sort(A, n)
print 'After sorted: ', A
- 最坏的情况(输入为逆序的序列)。
- 平均情况。
插入排序需要的辅助空间为 $O(1)$, 是一种稳定的排序算法。
5.2 归并排序¶
归并排序是一种分治问题,通过递归的方式来解决问题。在每一层的递归中,应用下面三个步骤:
- 分解:划分子问题,子问题和原问题一样,只是规模更小了。
- 解决:按照递归求解子问题。如果规模足够小了,则停止递归,直接求解。
- 合并:将子问题的解组合成原问题的解。
归并排序包括下面三个步骤。
 图1
图1关于求解递归式有三种方法:
- 代入法:我们猜测一个界,然后用数学归纳法证明这个界是正确的。
- 递归树法:将递归问题转换为一棵树,其结点表示不同层次的递归调用产生的代价。然后采用变价和技术来求解递归式。
- 主方法:可求解下面公式的递归式的界: $T(n)=aT(n/b)+f(n)$ , 其中 $a\geq1, b>1, f(n)$是一个给定函数。
在这节课上,主要介绍了使用递归树的方法来求解归并排序。
从上面归并排序的三个步骤分析,则有:
\begin{equation} T(n)= \left\{ \begin{array}{lr} \Theta(1), &if\ n = 1; \\ 2T(n/2) + \Theta(n), &if\ n> 1. \end{array} \right. \end{equation}现在引入递归树来求解 $T(n)=2T(n/2) + cn, 其中\ c > 0 为常数。$把上面的式子转换成一棵树。按照下面图 2~6 来推算。
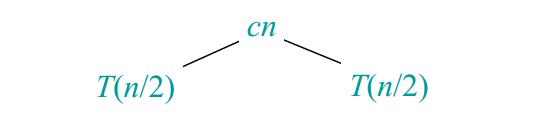 图2
图2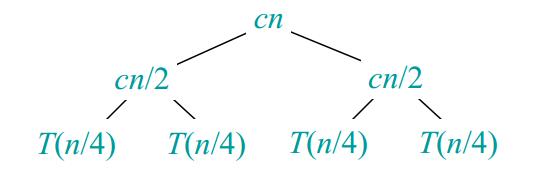 图3
图3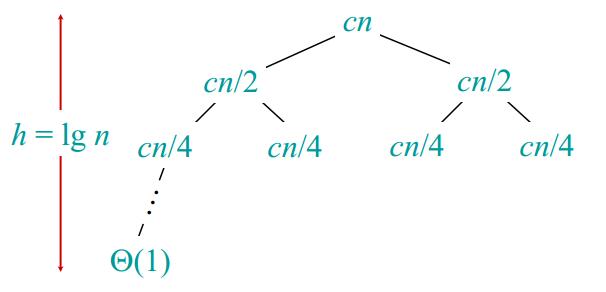 图4
图4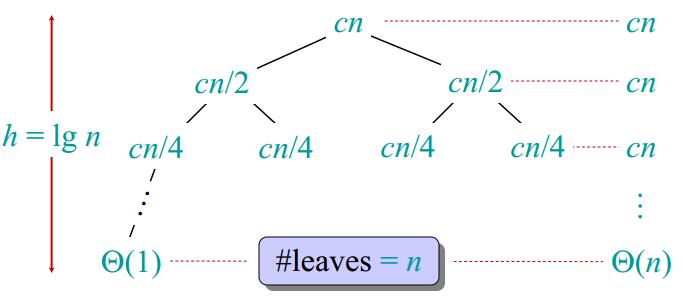 图5
图5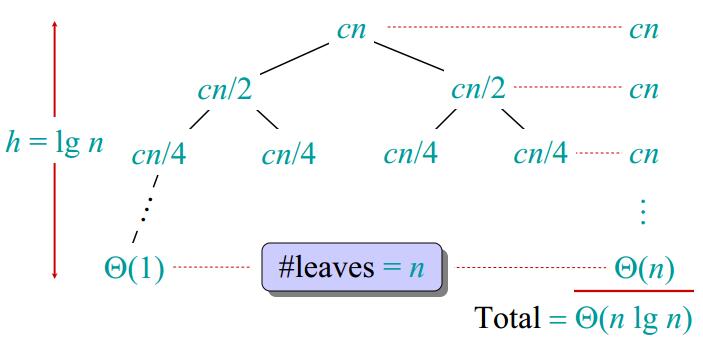 图6
图6所以归并排序的渐进时间复杂度为 $\Theta(nlgn)$,这比插入排序的 $\Theta(n^2)$ 增长要慢得多。实际上,当$n>30$的时候,归并排序优于插入排序。
下面是用 python 写的归并排序的代码。[2] 归并排序详解(python实现)
一共就两个函数。 "merge(a,b)" 函数将两个序列进行合并。"merge_sort(_list)" 函数,对序列 _list 从下(最小规模)往上进行合并排序。
# 归并排序
def merge(a,b):
"""a,b 是两个有序的序列,将a,b合并到c中返回。"""
c = list()
i = j = 0
while i < len(a) and j < len(b): # 若两个list中都还有元素
if a[i] < b[j]: # 从两者中选出较小的一个添加到 c 中
c.append(a[i])
i += 1
else:
c.append(b[j])
j += 1
if i == len(a): # 如果 a 已经全部添加到 c, 把 b 剩下的部分全部添加到 c 中
c.extend(b[j:])
else: # 否则 b 已经全部添加到 c 中,把 a 剩下的部分全部添加到 c 中
c.extend(a[i:])
return c
def merge_sort(_list):
"""用递归的方式来对整个序列 _list 进行合并排序。"""
if len(_list) <= 1: # 2.当只有一个元素的时候,直接求解。开始往上合并。
return _list
middle = len(_list) / 2 # 1.划分子序列。
left = merge_sort(_list[:middle])
right = merge_sort(_list[middle:])
return merge(left, right) # 3.合并子序列
# Eg:
A = [8, 2, 4, 9, 3, 6, 7]
n = len(A)
print 'Before sorted: ', A
A = merge_sort(A)
print 'After sorted: ', A
下面比较两个函数的实际运行效率:
import numpy as np
from time import time
size = 1000
list1 = np.random.randint(-100, 100, size)
time0 = time()
list_sorted = insert_sort(list1, size)
print 'Size: %d, Insert_sort costs %g seconds.'% (size, time() - time0)
time0 = time()
list_sorted = merge_sort(list1)
print 'Size: %d, Merge_sort costs %g seconds.'% (size, time() - time0)
size = 10000
list1 = np.random.randint(-100, 100, size)
time0 = time()
list_sorted = insert_sort(list1, size)
print 'Size: %d, Insert_sort costs %g seconds.'% (size, time() - time0)
time0 = time()
list_sorted = merge_sort(list1)
print 'Size: %d, Merge_sort costs %g seconds.'% (size, time() - time0)
从上面的结果来看,归并排序的运行时间要远远小于直接插入排序。
总结
- 掌握渐进分析方法。
- 掌握如何使用 递归树 的方法来求解递归问题的渐进时间复杂度。
- 熟练编写归并排序的代码。
参考
[1] MIT算法导论——第一讲.Analysis of algorithm
[2] 归并排序详解(python实现)