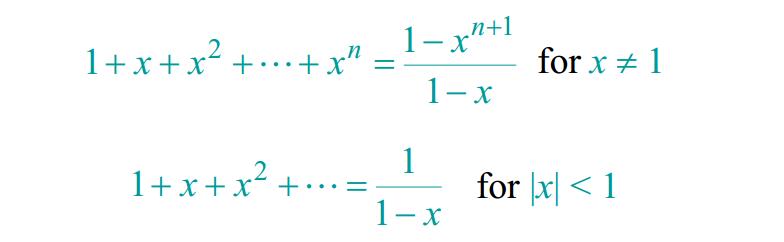Lecture-02 渐进记号及递归式求解
Jun 4, 2017
摘要:这节课介绍的是一些数学内容,完全没有涉及到具体的算法。内容可以分为两部分:1. 从定义上详细介绍几种渐进记号的意义。2.介绍递归式的三种求解方法:代入法,递归树法和主方法。
渐进记号
在第一节课上,我们已经接触到了渐进记号 $\Theta{n}$。在上节课中我们学习了渐进分析:
- 对于一个算法的运行时间,忽略那些依赖于机器的常量;
- 忽略所有的低阶项,只分析最高阶项;
- 关注于运行时间的增长,而不仅仅只是运行时间。不去考虑每个基本运算所消耗的时间。
在实际的算法分析中,我们定义了一些渐进记号来帮助我们更加方便地进行分析。下面是这些渐进记号的具体定义和实际意义。 一般我们会看到 $f(n)=O(g(n))$,这指出函数 $f(n)$ 是集合 $O(g(n))$ 的成员。注意这里的等号和平时看到的等号的意思可不一样。这里的表示属于的关系。
$O$记号,渐进地给出一个函数的上界。对于 $O(g(n)) $ 定义的函数集: 表示存在正常量 $c, n_0$,使得对于所有的 $n>n_0$,都满足 $0\leq{f(n)}\leq{cg(n)}$ 。
也就是说,$f(n)$的复杂度最多与$g(n)$一个数量级,即小于等于。例如,$2n^2 = O(n^3)$,表示$2n^2 \epsilon {O(n^3)}$。当然$2n^2 = O(n^2)$ 也是正确的。我们只需要取$c\geq{2}$ 即可满。
$\Omega$ 记号,渐进地给出一个函数的下界。对于 $\Omega{(g(n))} $ 定义的函数集: 表示存在正常量 $c, n_0$,使得对于所有的 $n>n_0$,都满足 $0\leq{cg(n)}\leq{f(n)}$ 。
也就是说,f(n)的复杂度最少与g(n)一个数量级,即大于等于。例如,$\sqrt{n} = \Omega{(lgn)}$,应该这样理解,对于充分大的$n$,$\sqrt{n} $至少是 $lgn$ 的常数倍。
$\Theta$ 记号。给出一个函数的渐进确界。对于 $\Theta{(g(n))} $ 定义的函数集: 表示存在正常量 $c_1, c_2, n_0$,使得对于所有的 $n>n_0$,都满足 $0\leq{c_1g(n)}\leq{f(n)}\leq{c_2g(n)}$ 。
也就是说,f(n)的复杂度与g(n)是同一个数量级,即等于。例如,$n^2 + O(n) = Θ(n^2)$ 是成立的,而$\sqrt{n} = Θ(lgn)$ 却是不成立的,因为 $\sqrt{n}$ 的确渐近地大于 $lgn$。
小结1:上面的给出了三个渐进符号的定义。在定义中,三个符号都是渐进趋正的,除此之外,我们可以这样记住三个符号的意义。
- $f(n) = O(g(n)) $ 表示 $f(n)$的复杂度至多与$g(n)$一个数量级,即$f(n)$小于等于$g(n)$。
- $f(n) = \Omega{(g(n))} $ 表示 $f(n)$的复杂度至少与$g(n)$一个数量级,即$f(n)$大于等于$g(n)$。
- $f(n) = \Theta{(g(n))} $ 表示 $f(n)$的复杂度与$g(n)$应该是同一个数量级,即$f(n)$等于$g(n)$(这里的大于,小于和等于指的都是数量级)。可见 $\Theta$ 是上面两个符号的并集。
上面我们提到,$2n^2 = O(n^3)$ 和 $2n^2 = O(n^2)$ 都是成立的。但前者不是渐进紧确的,而后者则是渐进紧确的。下面的两个渐进符号都是给出非渐进紧确的界。这两个渐进符号更多地用于求极限中。
$o$ 记号,给出一个函数的非渐进紧确上界。对于 $o{(g(n))} $ 定义的函数集: 表示存在正常量 $n_0$,使得对于任意的$c$, 当$n>n_0$时,都满足 $0\leq{cg(n)}\leq{f(n)}$ 。
例如,$2n = o(n^2)$,而 $2n^2 \neq o(n^2)$。
$ω$ 记号,给出一个函数的非渐进紧确下界。对于 $ω{(g(n))} $ 定义的函数集: 表示存在正常量 $n_0$,使得对于任意的$c$, 当$n>n_0$时,都满足 $0\leq{f(n)}\leq{cg(n)}$ 。
小结2: 这里给出的两个小写的渐进记号。和上面的大写的渐进记号相比,这里少了等于这部分。也就是给出的是非渐进紧确的上界或者下界。
- $f(n) = o(g(n)) $ 表示 $f(n)$的复杂度要比$g(n)$的数量级小,即小于。
- $f(n) = \omega{(g(n))} $ 表示 $f(n)$的复杂度要比$g(n)$的数量级大,即大于。
递归式的求解
关于求解递归式有三种方法:
- 代入法:我们猜测一个界,然后用数学归纳法证明这个界是正确的。
- 递归树法:将递归问题转换为一棵树,其结点表示不同层次的递归调用产生的代价。然后采用变价和技术来求解递归式。
- 主方法:可求解下面公式的递归式的界: $T(n)=aT(n/b)+f(n)$ , 其中 $a\geq1, b>1, f(n)$是一个给定函数。
在这三个方法中,前面两个方法是比较简单的,主方法的话稍微复杂一些,但是理解起来其实也不难。
代入法
代入法包括下面三个步骤:
1. 猜测该函数的界的形式。
2. 使用数学归纳法来验证 1 中的猜测是否正确。
3. 如果猜测正确的话,找出具体的常量和系数。
下面给出一个例子,通过求该函数的上界来说明代入法怎么用。
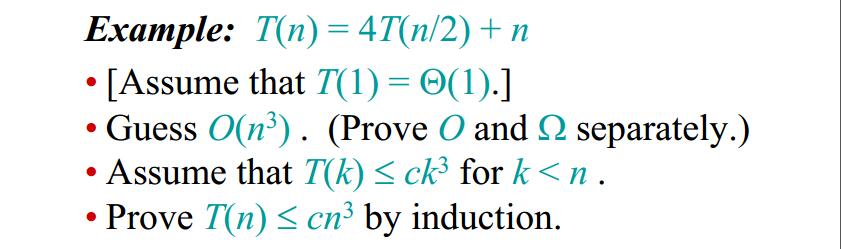

在上图中,我们证明了$T(n) = O(n^3)$,这里给出了函数的上界,但是并不是渐进紧确的上界。事实上$T(n) = O(n^2)$ 也是成立的,在课堂上老师也进行了证明。所以,通过上面的例子,我们证明了$T(n)$ 至多只能是 $O(n^3)$ .
递归树法
递归树法是一种非常直观,非常实用的方法。它最棒的一点就是总是能用,而且很直观的告诉你答案是多少,只是有些不严谨。在第一节课上,我们已经用过递归树来求解归并排序的渐进时间复杂度。在这节课中,老师给出了一个更加复杂的例子,但是一样很容易理解。
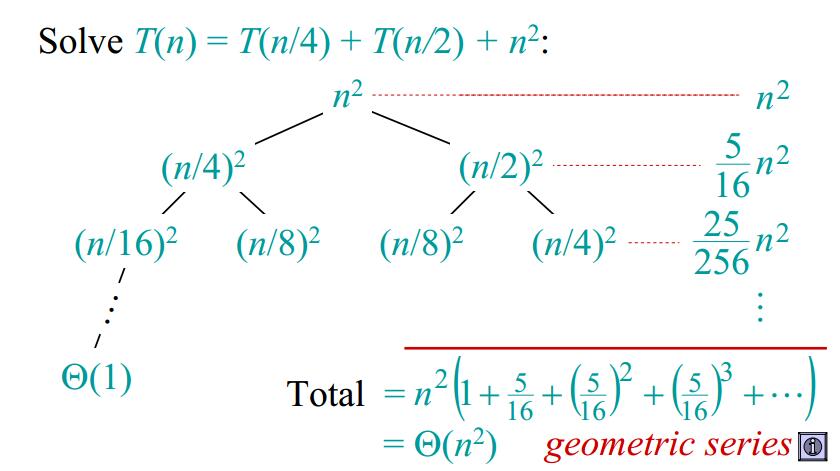
上图中,Total 等式的右边中有个等比数列,显然这个序列求和是小于2的,所以很容易地求解出结果为 $T(n) = \Theta{(n^2)}$。
主方法
和上面递归树的方法相比,主方法并没有这么直观,而且主方法还有非常严格的限制。但是它更加直接粗暴,因为主方法给出的是一个公式。我们只需要把递归函数带进来算一下就能够得到结果。
主方法只能求解下面形式的递归式的界。
其中,$a\geq1, b>1, f(n)$是一个给定函 数。
注意递归式中的右边只有一个时间函数。也就是说,每个式中只能有一个形式一致的子问题。
如果递归式符合上面形式的话,那么$T(n)$会有如下的渐进界:
Case1. 若对某个常数 $\varepsilon > 0$ 有 $f(n)=O(n^{log_ba-\varepsilon})$,也就是 $f(n)$ 比 $n^{log_ba}$ 增长要慢,则$T(n) = \Theta{(n^{log_ba})}$。
Case2. 若$f(n)=\Theta(n^{log_ba})$,也就是 $f(n)$ 和$n^{log_ba}$ 增长速度一致,则$T(n) = \Theta{(n^{log_ba}lgn)}$。
Case3. 若对于某个常数 $\varepsilon > 0$ 有$f(n)=\Omega(n^{log_ba+\varepsilon})$,也就是 $f(n)$ 比$n^{log_ba}$ 增长要快。且对某个常数 $c < 1$和所有足够大的 $n$ 有 $af(n/b) \leq cf(n)$,我们必须保证 $f(n)$ 的子问题要比原问题中小。则 $T(n)=\Theta(f(n))$。
当看到这里边凌乱的 $log, \Theta, \Omega$ 时,我的内心也是凌乱的,但是后面我们那出递归树来推一遍看看就知道是为什么了。下面先给出老师讲的四个例子,前面三个分别对应上面的三个 $case$,最后一个是主定理不适用的例子。
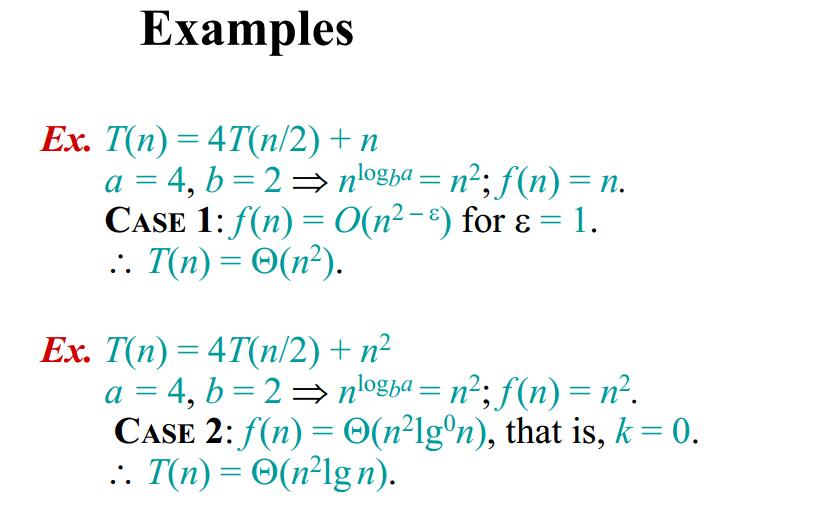

下面我们来用递归树法对主定理进行一个简单而形象的证明。在上面的三种情况中,我们注意到每个情况都是拿 $f(n)$ 和 $n^{log_ba}$ 来比较。这里的 $n^{log_ba}$ 其实就是叶子节点的数量。将主定理方法的递归式化成下面的递归树形式,树的高度为 $h$,每一层效率分析如右边列出所示。其中图中紫色方框中的内容即是叶子节点效率结果的数学推导。
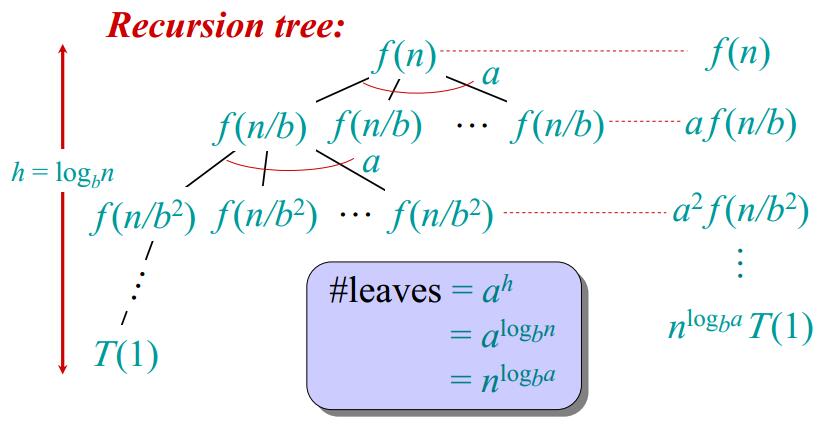
对于CASE 1,$f(n)$ 比 $n^{log_ba}$ 增长要慢,整个递归树的权重从根节点到叶节点一直增加,整个递归树的权重主要在叶子节点,$n^{log_ba}$ 占主导地位,所以$T(n) = \Theta{(n^{log_ba})}$。;
对于CASE 2,$f(n)$ 和$n^{log_ba}$ 增长速度一致,(k = 0,书中没有这个k,视频中讲了)。递归树每层的权重大致相同,总共 $h=lgn$ 层,所以整个递归树的权重将各层的权重加起来即可:$T(n) = \Theta{(n^{log_ba}lgn)}$。
对于CASE 3,则与CASE 1的情况正好相反,也就是 $f(n)$ 比$n^{log_ba}$ 增长要快,整个递归树的权重主要在根节点上,$f(n)$ 占主导地位,所以 $T(n)=\Theta(f(n))$
如上的分析,主定理方法的三种情况的结论便也不难理解。
总结:这节课主要介绍了渐进记号符的意义和三种求解递归式的方法。渐进分析是算法分析中非常有效的一种方法,而渐进记号符帮助我们很好地实现了这样的方法。在第二部分介绍的三种方法中,主方法给出了一个非常有效的求解公式,通过递归树的理解我们也明白了主定理的由来。但是我觉得递归树的方法更加直观容易,对于我这种记性差的人来说也是一个非常 nice 的选择呀。 虽然这节课没讲任何算法可能会有些无聊,但是对于后面学习各种算法的时候我们却非常需要这节课的内容来帮助分析,所以牢牢地掌握这节课的内容也是非常必要的呀。
附:等比数列求和公式