Lecture-03 分治算法
Jun 4, 2017
摘要:这节课主要介绍了分治算法的思想及其应用,结合前面一节课中所学习的主定理来对一些实例进行分析。这节课上介绍了下面这些例子:归并排序,二分查找,乘方问题,斐波那契数列,矩阵乘法,VLSI(超大规模集成电路)最小面积布线。本文将阐释各个例子的求解,并使用 python 对部分例子进行实现。
在第一次课上就介绍了归并排序,它利用了分治策略。在分治策略中,我们递归的解决一个问题,在每一层的递归中应用如下三个步骤:
- 分(Divide),即将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小。
- 治(Couquer),即递归地解决子问题。如果子问题的规模足够小,则停止递归,直接求解。
- 合并(Combine),即将子问题的解组合成原问题的解。
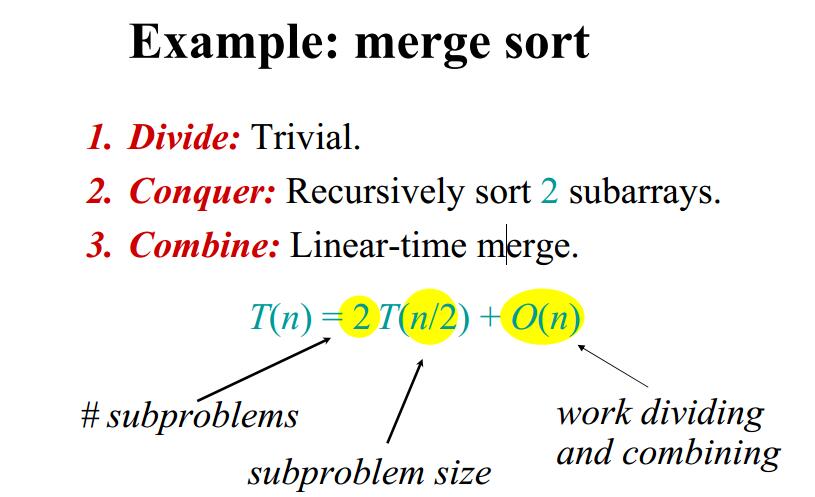
归并排序
在归并排序中:
分:把待排序的序列分为两个子序列进行排序。
治:递归地继续把子序列分成更小的序列,直到子序列长度为1。这时候子序列一定有序。每个 $T(n)$ 包括两个 $T(n/2)$.
合并:将两个有序的子序列合并成一个有序的数列,复杂度为 $f(n) = \Theta{(n)}$。
利用主定理很容易就求解出归并排序的时间复杂度为 $\Theta(nlgn)$。(在算法导论书中,默认 $lgn=log_2n$)。
二分查找
二分查找的前提是有序的数组。
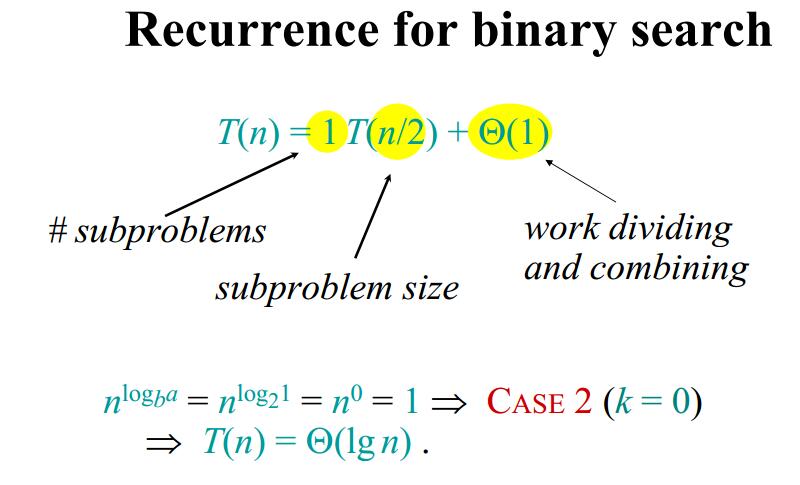
分:查找数组的中间元素。
治:如果查找的元素不对的话,递归地在左边子序列或者右边子序列继续查找。每个 $T(n)$ 包括1个 $T(n/2)$.
合并:将查找到的元素返回。 $f(n) = \Theta{(1)}$。
利用主定理很容易求解出二分查找的时间复杂度为 $\Theta(lgn)$。
def binary_search(sorted_list, left, right, key):
"""二分查找。"""
if left > right:
return -1
middle = left + (right - left) / 2
if sorted_list[middle] == key:
return middle
if sorted_list[middle] > key:
right = middle - 1
return binary_search(sorted_list, left, right, key)
left = middle + 1
return binary_search(sorted_list, left, right, key)
def search(sorted_list, key):
"""sorted_list 是一个由小到大排序好的数组,找到 key 在数组中的下标,如果 key 不在数组中,返回 -1"""
left = 0
right = len(sorted_list) - 1
return binary_search(sorted_list, left, right, key)
if __name__ == "__main__":
a = [1,3,12,34,44,66,234, 922]
key = 922
print search(a, key)
key = 4
print search(a, key)
7
-1
计算乘方
如果直接计算乘法 $a^n$,就是进行 $n-1$ 次乘法,显然有 $T(n) = \Theta(n)$。但是我们可以利用分治的思想。

分:把 $n$ 次乘法分成两部分来计算,如上图所示,因为两部分是相同的,所以我们只需要算一遍,即每个 $T(n) 包含一个 T(n/2)$。
治:继续分解,直到每部分只有一个 $a$。
合并:将两部分计算的结果相乘。 $f(n) = \Theta{(1)}$。
利用主定理很容易求解出二分查找的时间复杂度为 $\Theta(lgn)$。
def power(a, n):
"""递归计算 a 的 n 次方。"""
if n == 1:
return a
if n == (n >> 1 << 1): # n为偶数
r = power(a, n/2)
return r * r
# 否则为奇数
r = power(a, (n-1)/2)
return r * r * a
if __name__ == "__main__":
print power(2, 10)
print power(2, 11)
1024
2048
斐波那契数列(Computing Fibonacci numbers)
斐波那契数列是非常有名,也非常容易理解的一个序列,定义如下:
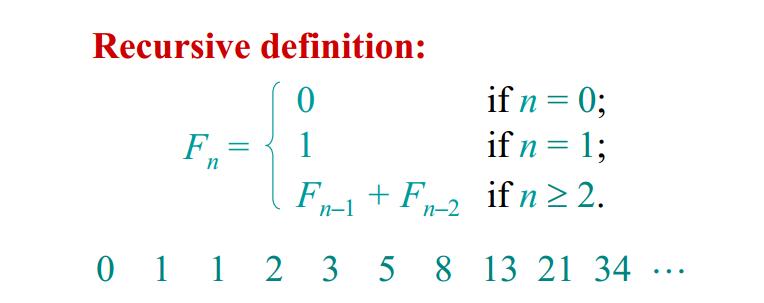
1.朴素递归算法(Naive recursive algorithm)
按照上面的定义中,我们通过递归地计算 $F_{n-1} 和 F_{n-2} 来得到 F_{n}$,这个算法的复杂度是指数级别的 $Ω(φ^n)$。其中$φ = (1 + 5^{½}) / 2$,即黄金分割比率。
2.朴素递归平方算法(Naive recursive squaring)
这个算法主要根据斐波那契数列的一条数学性质而来。该性质表明,斐波那契数列 $F(n)=round(φ^n / 5^½)$ ,即取 $(φ^n / 5^½)$ 最近的整数。这样,问题的求解于是变成了一个求乘方的问题,所以算法的效率为Θ(lgn)。
但是这个方法在实际上是不可行的的,主要是当n比较大时,由于硬件的限制,计算机中的浮点运算精度有限,所以算出来的结果会有误差。
3.自底向上算法(Bottom-up) 考虑到1中的简单递归算法,为了求解 $F(n)$,需要同时递归求解 $F_{n - 1}$ 和 $F_{n - 2}$,显然这样就做了大量的重复工作。采用自底向上的算法即可避免这样的冗余。要计算 $F_n$,则依次计算 $F_0,F_1,F_2 … F_n$,这时计算 $F_n$ 只需要利用前两个结果即可,这样算法效率提高到了$Θ(n)$。
4.递归平方算法(Recursive squaring)
该算法也是基于一个定理,定理以及证明过程如下图所示。这样,问题的求解即成为了矩阵的乘方问题,算法效率于是提高到了 $Θ(lgn)$。

矩阵乘法

1.常规算法(Standard algorithm)
矩阵的乘法,首先想到的当然就是如下的算法,不难看出该算法的效率为 $Θ(n^3)$。
for i in xrange(n):
for j in xrange(n):
C[i, j] = 0
for k in xrange(n):
C[i, j] += A[i, k] * B[k, j]
2.分治法算法(Divide-and-conquer algorithm) 矩阵乘法中采用分治法,第一感觉上应该能够有效的提高算法的效率。如下图所示分治法方案,以及对该算法的效率分析。结果利用主定理分析,算法效率还是$Θ(n^3)$。算法效率并没有提高。
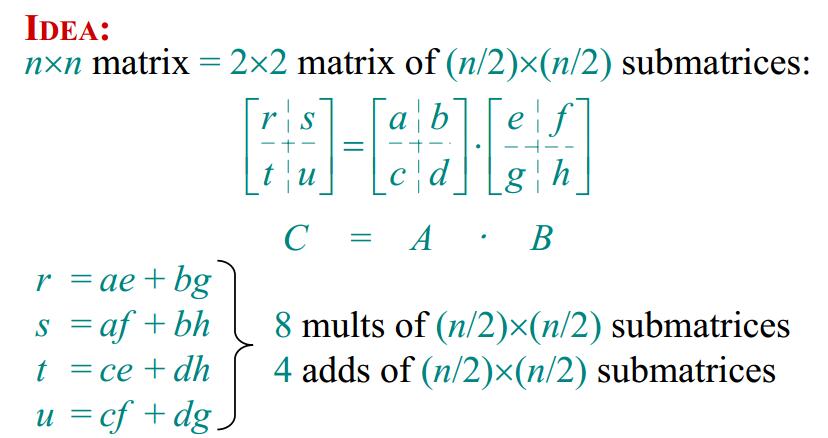
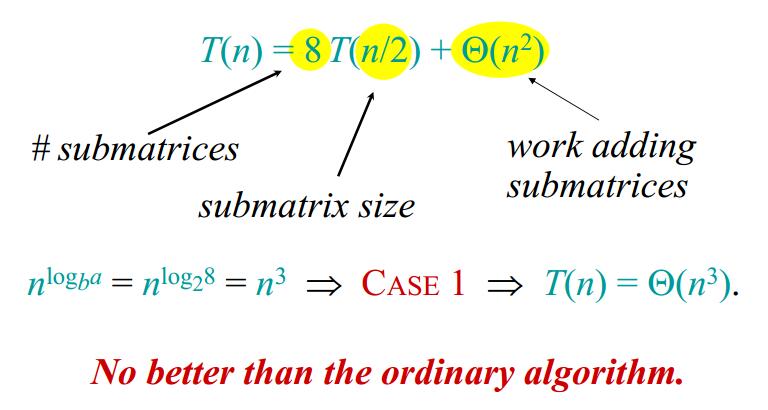
3.Strassen算法(Strassen’s algorithm)
在方法 2 中,我们利用主定理方法来分析出要想降低复杂度的话,应该设法把 $T(n/2)$ 的系数变得小一些。上面这个系数表示矩阵相乘的次数,所以我们要设法减少乘法的次数。Strassen提出了一种将系数减少到7的分治法方案,如下图所示。

很难想象Strassen是如何想出这个方案的,不过它确实将原来递归式中系数由8减小到了7。如下图所示是该算法的算法效率分析:
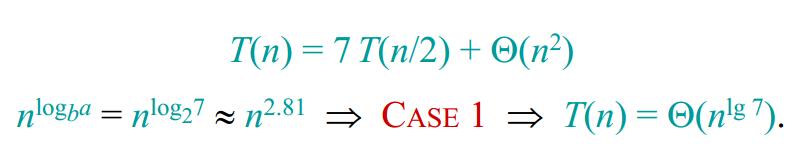
这样,Strassen算法将矩阵的乘法效率提高到了$Θ(n^{2.81})$。尽管这个2.81在数字上看起来并没有提高多少,但是由于算法效率本身就是指数级的,所以当n比较大时($n ≥ 32$ )在现代的机器上,Strassen算法的优势便已经很明显了。
当然,还有很多关于矩阵运算的优化算法。现在理论上矩阵乘法的效率最好的是:$Θ(n^{2.376…})$。但是在这众多的优化算法中,Strassen算法却是最简单的。
超大规模集成电路布线(VLSI layout)
问题描述:假设电路是一棵完全二叉树,一共有 n 个叶子节点。我们在格点图上进行电路布线,所有的边不能重合,要求最小的布线面积(矩形的面积)。
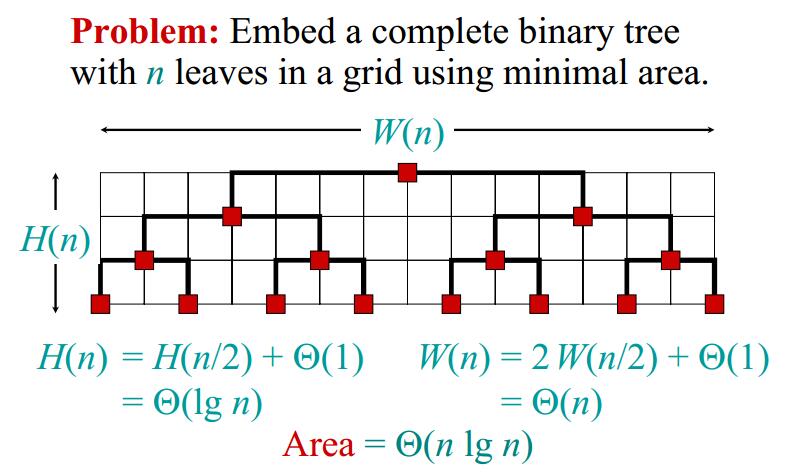
我们看到, $H(n) = \Theta(lgn), W(n) = \Theta(n)$,所以 $Area = \Theta(nlgn)$。 但是上面的布线中,我们看到还有很多地方是空着的,有没有方法能够使得布线更加紧密一些,使得 $Area = \Theta(n)$ 呢?假设 $H(n) = \Theta(\sqrt{n}), W(n) = \Theta(\sqrt{n})$,那么就有 $Area = \Theta(n)$ 了。
根据主定理,要是 $n^{log_ba} = n^{1/2}$, 则 $log_ba = 1/2$,比如取 $a = 2, b = 4$。
即把叶子节点分成 2 部分摆放, 每部分的宽度为原来的 1/2 ,如下图所示.
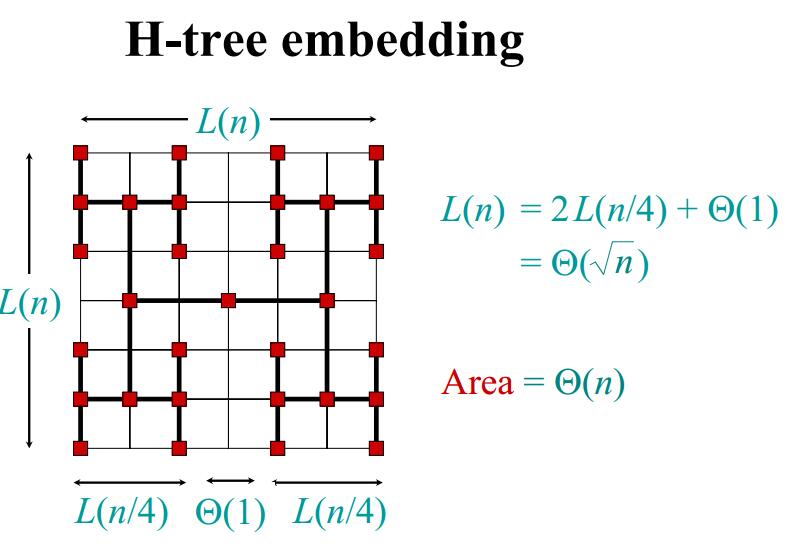
总结: 这节课介绍了几个分治算法,并利用上一节课上学到的主定理对它们进行了复杂度分析。可以看到在递归问题中,记住主方法能够帮助我们迅速地分析出算法的时间复杂度。这节课的内容比较简单,最主要的是掌握 分 -> 治 -> 合并的思想。关于递归算法的代码实现也比较容易,自己动手实现两个算法就能熟悉这个“套路”了。