Lecture-04 快速排序算法

Jun 5, 2017

摘要：这节课主要介绍了快速排序算法并对其进行时间复杂度分析。1.介绍了快速算法的具体实现并给出相应的代码实现。2.算法时间复杂度分析：最坏情况分析，最优情况分析，平均情况分析。3.随机化快速排序算法及其时间复杂度分析。其中前面两点理解起来很容易，第三点中分析随机化快速排序算法的复杂度理解起来比较困难。本文主要介绍快排算法的实现，至于复杂度的分析只做一些课堂疑难点记录。

快速排序算法

快速排序由Tony Hoare在1962年提出。

基于分治思想(Divide-and-conquer)
原地排序。所谓原地排序，即指算法的空间复杂度为O(1)，它就在原来的数据区域内进行重排。就像插入排序一样，就在原地完成排序。但是归并排序就不一样，它则需要额外的空间来进行归并排序操作。
实用性很强。实际应用中，一般按照一些标准的步骤对基础的快排算法进行一些微调既可以达到非常高的效率。在实际中快排通常比归并排序要快 3 倍以上。（老师原话）

快排中使用了分治策略。

分：选择一个主元素（$pivot = x$）,把原来待排序的序列分为两个子序列。左边子序列所有元素小于 $x$, 右边子序列所有元素大于 $x$。治：递归地对左右两个子序列进行排序。合并：上面两步结束后就已经了排序。

快速排序里面最关键的就是第一步：分化（Partition）的步骤，这是该算法处理问题的核心。所以我们可以把快排看成是递归地划分数组，就想归并排序是递归地合并数组一样。关于Paritition的具体算法，目前有好几种，其伪代码稍有不同但是它们的原理都是一样的。当然最重要的一点是它们的算法复杂度都是线性的，也就是$O(n)$。

1、最坏情况下分析当输入序列是正序或者是反序的时候，因为这时候分划总是围绕着最大的或者是最小的元素进行，那么造成的现象就是分划的另外一边总是没有元素，这样就无法利用递归来提高算法运算的效率。

那么，在这种情况下，快排的算法效率递归式如下图所示，易知这时的效率是$Θ(n^2)$。

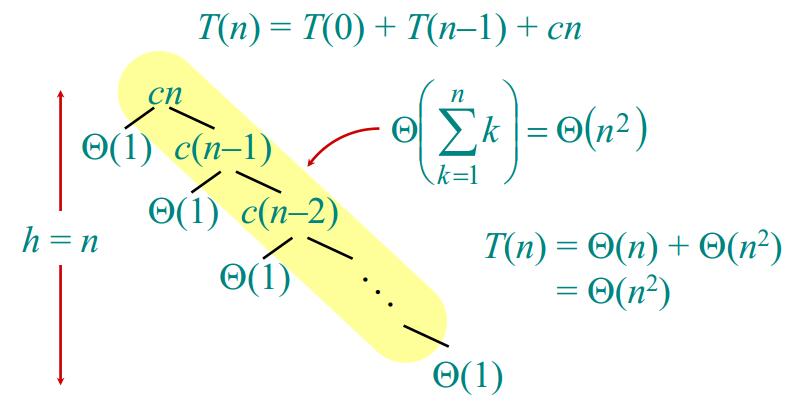
2、最优情况下分析我们当然没有办法保证输入序列能够满足快排的最优情况，但是我们可以这样直观地来理解：如果我们足够幸运，Partition每次分划的时候正好将数组划分成了两个相等的子数组。那么这种情况下的递归分析式如下图所示。

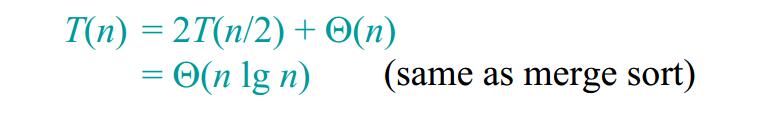
这显然是我们想要的结果。那么当Partition的时候达不到均等地划分，如果两个子数列划分的比例是1:9呢？

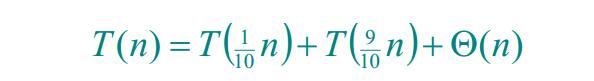
为了解这个递归式，主方法是派不上用场了。这时候搬出总是能够有效的分析树，如下图所示。

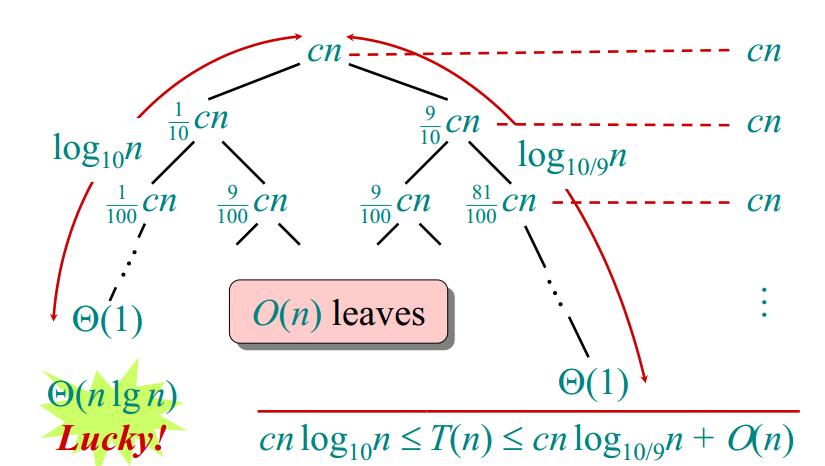
综上所述，可以知道快排在最优情况下的算法效率是$Θ(nlgn)$。注：$log_{10/9}n=\dfrac{lgn}{lg(10/9)} \approx 6.58lgn$

3、平衡划分情况分析

快排的平均运行时间更接近于其最优情况，而非最差情况。由于好和坏的划分是随机分布的。基于直觉，我们假设算法中最坏与最优情况交替出现，那么算法的效率分析如下图所示。

可以得知，在这样的情况下我们也还是幸运的，得到的算法效率与最优情况下的效率一样。那么我们如何保证我们总是幸运的呢？这也是随机化快速排序需要解决的问题。

随机化快速排序

我们已经知道，若输入本身已被排序，那么对于快排来说就糟了。那么如何避免这样的情况？一种方法时随机排列序列中的元素；另一种方法时随机地选择主元（pivot）。这便是随机化快速排序的思想，这种快排的好处是：其运行时间不依赖于输入序列的顺序。也就是说我们不再需要对输入序列的分布作任何假设，没有任何一种特定的输入序列能够使算法的效率极低。最不幸运的情况有可能会发生，但是也是因为随机数产生器的原因，不是因为输入序列的原因。

这里的办法是随机地选择主元。如下图所示是随机化快速排序的算法效率递归表达式。

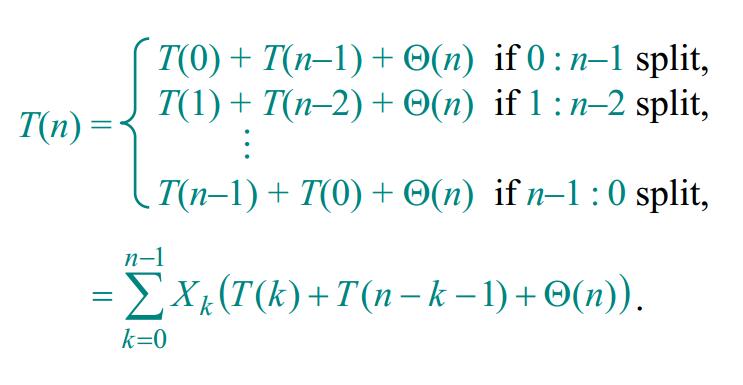
这里要注意，$X_k$ 是独立于 $T(k)$ 的，因为$X_k \epsilon {0, 1}$ 表示本次选择的 pivot 分成的子序列中左边序列是否有 k 个元素。而 $T(k)$ 表示子问题的递归，这和 $X_k$ 是没关的。具体的复杂度分析可以看课件。

基础版快排python实现

伪代码如下：

下面python代码实现和课堂上老师讲的方法有一点不太一样，但并不影响。主要是每一趟找 pivot 位置时的思路有点不同，主要是我习惯这种写法了。

def partion(nums, p, r):
    """nums 是一个序列，我们以第一个元素 nums[0] 为主元，进行一趟排序。"""
    key = nums[p]
    left = p
    right = r
    while left < right:
        while (left < right) and (nums[right] >= key):  # 从右向左扫描，找到一个比 key 小的元素
            right -= 1
        nums[left] = nums[right]
        while (left < right) and (nums[left] <= key): # 从左向右扫描，找一个比 key 大 的元素
            left += 1
        nums[right] = nums[left]
    nums[left] = key
    return left

def qsort(nums, p, r):
    """对序列 nums[p:r+1] 进行排序。"""
    if p < r:
        i = partion(nums, p, r)
        qsort(nums, p, i-1)
        qsort(nums, i+1, r)
        
if __name__ == '__main__':
    nums = [8,10,9,6,4,16,5,13,26,18,2,45,34,23,1,7,3]
    print nums
    qsort(nums,0,len(nums)-1)
    print nums

[8, 10, 9, 6, 4, 16, 5, 13, 26, 18, 2, 45, 34, 23, 1, 7, 3]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 13, 16, 18, 23, 26, 34, 45]